May 2023 / INVESTMENT INSIGHTS
The Art of Actively Managing Interest Rate Risk
With volatility likely to persist, an active approach remains critical
Key Insights
- Given the highly uncertain investment environment, we believe that interest rate risk will continue to be a source of investment volatility that needs to be actively managed.
- Empirical duration can be a better practical measure of interest rate risk, in our view, as analytical duration tends to oversimplify price sensitivity and ignores real‑life variables.
- Active interest rate management should go beyond managing duration as risks and alpha opportunities can also be found in country selection, convexity, curve positioning, and security selection.
Managing interest rate risk continues to remain of critical importance as volatility looks set to persist amid a highly uncertain backdrop of sticky inflation, slowing growth, tighter central bank policy, and banking sector worries.
For several years, many fixed income managers have assumed that better information ratios could be achieved through active credit decisions rather than managing interest rate risk. Up until last year, that approach generally worked as very supportive central banks dominated the post financial crisis era and kept rate volatility muted. But with central banks retreating, the environment has changed, meaning those days of artificially low interest rate volatility are likely behind us now.
Interest rate volatility rose significantly in 2022, fueled by inflation surprises and central banks unleashing their most aggressive hiking cycles for more than two decades. While there was some hope that interest rate volatility could ease slightly this year, banking sector concerns have added a new uncertainty to an already challenging set of issues facing markets. Against this highly uncertain backdrop, we believe that interest rate risk will continue to be a source of investment volatility that needs to be actively managed going forward, particularly in the absence of central bank support, there is no buyer of last resort to help keep interest rate volatility suppressed.
Here at T. Rowe Price, we proudly describe ourselves as active interest rate managers. In this paper, we provide details about the important variables that we believe should be considered when managing interest rate risk.
Interest Rate Volatility Remains Elevated
(Fig. 1) Levels of the MOVE Index since early 2000

As of March 31, 2023.
Past performance is not a reliable indicator of future performance.
The date range is April 7, 2000 to March 31, 2023.
MOVE—ICE BofA MOVE Index represents implied volatility on 1‑month Treasury options.
Source: Bloomberg Finance L.P.
Analytical Duration Ignores Real‑Life Variables
There are multiple ways to measure interest rate risk, with the most common being analytical duration measures, such as modified or effective duration. However, analytical duration in a global fixed income portfolio has limited explanatory power of actual interest rate risk. That’s because it largely oversimplifies the price sensitivity of a fixed income portfolio, particularly if it’s globally diversified and/or consists of multiple sectors. Analytical duration also doesn’t capture a bond’s convexity—an important measure of the nonlinear relationship of a bond’s price to interest rate changes—which we will go into in more detail later in the paper.
We believe that analyzing empirical duration alongside analytical duration will improve our understanding of how portfolios will be affected by yield changes. Empirical duration calculates a bond’s duration based on historical data rather than a preset formula, like effective duration does. It uses regression analysis of historical market‑based bond prices and U.S. Treasury yields to estimate a bond’s empirical duration.
Put simply, by looking at the historical relationship, empirical duration indicates how sensitive a bond price will be to changes in a reference bond yield, most commonly U.S. Treasuries. This sensitivity will vary depending on variables such as spread levels, idiosyncratic factors, and technicals.
Empirical duration, while an efficient indicator of price sensitivity, relies on the assumption that history is a strong guide to the future. Regression analysis can sometimes be sensitive to the period used, so different time periods generate different results. Therefore, we calculate empirical duration using multiple‑period lookbacks. This helps us to observe the stability of the regression over different time frames as well as observe if there’s a change using shorter, more recent history.
It Is Crucial to Look Beyond Duration
Empirical duration is a good starting point, but it too has drawbacks. We believe that to effectively manage interest rate risks, it’s important to go beyond duration as risks and alpha opportunities can also be found in country selection, convexity, curve positioning, and security selection.
Correlations Vary and Are Unstable Over Time
Global fixed income portfolios typically consist of allocations to multiple sovereign curves. How they correlate to each other may vary widely. For example, the Canadian sovereign curve typically has the highest and most stable correlation to the U.S. Treasury curve. Other countries’ correlations vary widely and are often unstable over time, as depicted in Figure 2.
Bond Correlations Unstable Over Time
(Fig. 2) Monthly yield correlations of different sovereign bonds to U.S. Treasuries

As of November 30, 2022.
Past performance is not a reliable indicator of future performance.
The chart shows monthly yield correlations of different 10‑year sovereign bonds to the U.S. 10‑year Treasury bond over 12‑month rolling periods.
Source: Bloomberg Finance L.P.
The reasons that correlations vary between countries include fundamental factors unique to each country (such as inflation and fiscal balance) and market factors (such as international buyer penetration and domestic support). While it’s important to understand the historical relationships, an effective interest rate manager also needs to consider how current factors might impact these relationships today. That’s why individual country analysis is essential, in our view.
The Importance of Convexity
The relationship between price and yield is convex, which is why it’s important to also assess convexity when managing interest rate risk. As outlined earlier, analytical duration ignores convexity and assumes a linear relationship. For small changes in yield, that might be ok, but ignoring convexity when there are large changes in yield, will typically underestimate the price of a noncallable, option‑free bond. This is because duration is a tangent line to the price‑to‑yield curve at the calculated point, and the difference between the duration tangent line and the price‑to‑yield curve increases as the yield moves further away in either direction from the point of tangency.
Convexity is the rate that duration changes along the price‑to‑yield curve. Thus, it is the first derivative to the equation for duration and the second derivative to the equation for the price‑to‑yield function. Convexity is always positive for vanilla bonds. Furthermore, the price‑to‑yield curve flattens out at higher interest rates, so convexity is usually greater on the upside than on the downside. This means that the absolute change in price for a given change in yield will be slightly greater when yields decline rather than when they increase. Consequently, bonds with higher convexity will typically have greater capital gains for a given fall in yields than the corresponding capital losses that would occur when yields rise. As such, convexity is an attractive feature, and securities with high levels of convexity will typically demand a premium as a result.
Understanding Bond Convexity
(Fig. 3) Illustration of possible error when estimating bond price based only on duration
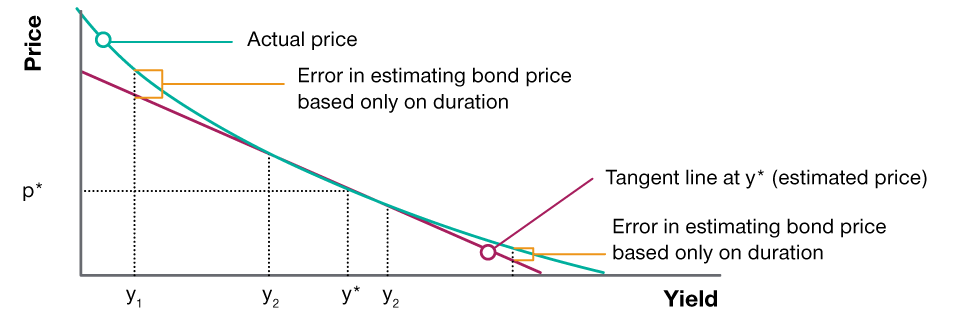
As of March 31, 2023.
For illustrative purposes only.
Source: T. Rowe Price.
Conversely, securities that have callable features tend to have negative convexity, and the holder of these bonds usually requires a premium for these less favorable characteristics. With a callable bond, as interest rates fall, the incentive for the issuer to call the bond at par increases; therefore, its price will not rise as quickly as the price of a noncallable bond. The price of a callable bond might actually drop as the likelihood that the bond will be called increases. This is why the shape of a callable bond’s curve of price with respect to yield is typically concave or negatively convex.
While we generally prefer bonds with positive convexity, it may be appealing to invest in negatively convex bonds if the potential premium received outweighs the negative impact from the bond’s price response to yield changes.
Curve Positioning Matters
Often, where you are positioned on interest rate curves is a very important factor in determining interest rate risk. 2022 was a year where sovereign curves in most countries experienced significant flattening or, in some cases, curve inversion. The yield change for shorter‑dated maturity bonds was much more significant than longer‑dated bonds. Key rate duration calculates the change in a bond’s price in relation to a 100‑basis‑point change in the yield for a given maturity. When yield curves shift in nonparallel fashion, key rate duration measures are more accurate in assessing interest rate risk.
Different parts of the curve are influenced by different factors, with the front end of the curve influenced largely by central bank rates. Technically, longer‑dated yields are an extrapolation of short‑term rates over time plus a term premium. The further you move out the curve, however, the more significant longer‑term growth and inflation expectations are in dictating the direction of yields. Technicals can also play a role. For example, the UK pension market has been a long‑term supporter of very long‑dated gilts, resulting in curve inversion at the back end. An effective interest rate manager should consider these factors and position a portfolio’s interest rate exposures at the most attractive key rates and away from those potentially more susceptible to capital loss.
It’s also worth noting that inverted yield curves have unattractive carry and roll‑down characteristics versus more normal‑shaped curves. This should also be considered when taking longer‑dated positions on inverted curves.
Instrument Choice Is a Key Consideration
Instrument selection is another important factor to consider when managing interest rate risk as different tools have different benefits and drawbacks. Often, the most efficient way to execute a view on interest rates is through derivatives because managers can alter a portfolio’s sensitivity to key rates without significant cash commitment or trading of the underlying bonds.
Government bond futures and swaps are often referred to as delta one derivatives because their profit and loss is, in general, lineally related to the underlying bond price. The most commonly used include interest rate futures and interest rate swaps. While interest rate swaps are over‑the‑counter derivatives, government bond futures are exchange‑traded. After the global financial crisis, U.S. regulations required interest rate swaps to be cleared in an effort to reduce counterparty risk. This resulted in trading cost increases, which typically makes them more expensive than government bond futures.
Interest rate swaps, however, are normally a purer reflection of interest rate risk than government bond futures. That’s because government bond futures can have varying duration, dollar valuation, and convexity depending on what underlying contract is the cheapest to deliver. There is also a limited range of maturities with government bond futures (2‑, 3‑, 5‑, and 10‑year and ultralong). These all have defined maturity ranges for the deliverable basket, so the bond future maturity can be anywhere in this range when entering the contract. There is also a need to roll government bond futures every three months as liquidity tends to be in the front‑month contract. This roll process incurs additional trading costs relative to the interest rate swap.
If a convex payoff is desired, which is usually the case for hedging tail risks but can also be used for speculation purposes, options are often used. These include options on bond futures or options on interest rate swaps (swaptions). The cost of these options is largely driven by strike price, time to maturity, and market volatility. Due to the changing deltas of these instruments, a portfolio’s interest rate risk can change meaningfully as the option moves further into or out of the money.
Rate Volatility to Remain High
We believe that the days of artificially low interest rate volatility are likely over as central banks are no longer supporting markets with quantitative easing. That, together with the array of other uncertainties and challenges that markets face at present, means that interest rate risk will likely continue to be a source of investment volatility in 2023 that needs to be actively managed. But as outlined, it’s important to go beyond just managing duration levels in a portfolio. That’s because risks and alpha opportunities can also be found in country selection, convexity, curve positioning, and security selection, which is why we consider these important variables in our approach to active interest rate management.
IMPORTANT INFORMATION
This material is being furnished for general informational and/or marketing purposes only. The material does not constitute or undertake to give advice of any nature, including fiduciary investment advice, nor is it intended to serve as the primary basis for an investment decision. Prospective investors are recommended to seek independent legal, financial and tax advice before making any investment decision. T. Rowe Price group of companies including T. Rowe Price Associates, Inc. and/or its affiliates receive revenue from T. Rowe Price investment products and services. Past performance is not a reliable indicator of future performance. The value of an investment and any income from it can go down as well as up. Investors may get back less than the amount invested.
The material does not constitute a distribution, an offer, an invitation, a personal or general recommendation or solicitation to sell or buy any securities in any jurisdiction or to conduct any particular investment activity. The material has not been reviewed by any regulatory authority in any jurisdiction.
Information and opinions presented have been obtained or derived from sources believed to be reliable and current; however, we cannot guarantee the sources’ accuracy or completeness. There is no guarantee that any forecasts made will come to pass. The views contained herein are as of the date noted on the material and are subject to change without notice; these views may differ from those of other T. Rowe Price group companies and/or associates. Under no circumstances should the material, in whole or in part, be copied or redistributed without consent from T. Rowe Price.
The material is not intended for use by persons in jurisdictions which prohibit or restrict the distribution of the material and in certain countries the material is provided upon specific request. It is not intended for distribution to retail investors in any jurisdiction.

